Project
Extraction Processes in Pump-Mixers – Development of a Coupled Cfd and Pbm Simulation Method to Investigate the Effects of Various Input Conditions on the Dispersion Generation
The focus of this project period was the flow simulation of pump-mixers which are apparatuses used for combined dispersion generation and pumping in technical liquid-liquid extraction processes. Since the mass transfer rate between the two phases is related to the surface area of the dispersed droplets, the control of the Droplet Size Distribution (DSD) is of utmost interest for process optimization. Hence, the aim of this project period was the enhancement of simulation methods for an a priori prediction of the DSD. Special emphasis was put on the influence of the turbulence model and the droplet-droplet interaction. A parameter study in terms of various integral volume fractions of the dispersed phase as well as the rotational speed of the stirrer was performed.
Project Details
Project term
March 1, 2022–April 30, 2023
Affiliations
Ruhr University Bochum
Institute
Chair of Hydraulic Fluid Machinery
Principal Investigator
Methods
A tank stirred by a Rushton turbine, which is a simplified version of a pump-mixer as shown in Figure 1, was considered. The fluid was a liquid-liquid dispersion consisting of paraffin oil droplets dispersed in a continuous water phase. A homogeneous Euler-Euler mixture approach was applied, which means that both phases are approximated as interpenetrating Eulerian phases. Simulations were performed with a pressure-based flow solver employing the Pressure-Implicit with Splitting of Operators (PISO) [1] scheme, which is a modified pressure-correction predictor-corrector step algorithm, whereby corrector steps are omitted, facilitated by small time steps and an additional deferred correction loop. Details can be found, e.g., in the publications by Issa [1] and Jasak [2] as well as in our recent publications by Hundshagen et al. [3] and Rave et al. [4,5]. 3D Computational Fluid Dynamics (CFD) is coupled to a Population Balance Model (PBM) for a prediction of the DSD. Transient simulations were conducted in the full 360° domain. A computational grid with 3.1 million cells was employed. Scale-Adaptive Simulations (SAS) with the model by Egorov & Menter [6] were performed to assess the effect of turbulence scale resolution on the DSD. Results were compared to the statistical Shear Stress Transport (SST) model by Menter [7]. Coalescence and breakup of the oil droplets were approximated on the sub-grid scale by the simple kernels by Coulaloglou & Tavlarides [8] and Hsia & Tavlarides [9]. Both kernels require a test-case specific model parameter calibration on experimental data. Experiments had been conducted by our project partners at the Chair of Separation Science and Technology and at the Laboratory of Reaction and Fluid Process Engineering, which are both located at the Technical University Kaiserslautern.
Results
Our latest results have recently been published by Rave et al. [5] and the reader is kindly referred to the publication for further details beyond this report. In Figure 2, time-averaged characteristic diameters of the DSDs simulated with both the SAS and SST models are shown and compared to experimental measurement data. The mean droplet size is expressed in terms of the Sauter mean diameter 𝑑̅32 The width of the distribution is expressed in terms of the interquantile range (IQR) being the difference between the percentiles 𝑑̅90,3 and 𝑑̅10,3, which is represented by a vertical bar bounded by two horizontal caps. The corresponding DSDs belong to the two distinct probe locations ML-I and ML-T which were positioned near the impeller blade and the liquid surface as depicted in Figure 1b), respectively. In the experiments, both the 𝑑̅32 and IQR increased with decreasing rotational speed N and increasing integral volume fraction Adis at both measurement locations. The trends are captured by both the SST and SAS turbulence models. However, with an increasing distance to the calibration point of the kernel parameter set at N = 400 [rpm] and Adis = 0.05, the difference to the experimental data becomes more pronounced. At all operating points, the characteristic diameters as well as the IQRs predicted by the SAS model are larger compared to the SST model. Both effects can be attributed to the notably lower turbulent energy dissipation rate (TEDR) predicted by the SAS model, which is a decisive input parameter in the breakup and coalescence kernels and causes an increase of the characteristic time scale for droplet breakup 𝜏b for droplets of all sizes. An increase of 𝜏b causes the droplets to remain larger than for the SST model, increasing the 𝑑̅32 Additionally, an increased 𝜏b causes a larger size range of droplets to be unaffected by droplet breakup, leading to a broader DSD in terms of a larger IQR compared to the SST model. Moreover, the DSDs evaluated at both measurement locations are closer to each other for the SAS model in comparison to the SST model which is in agreement with experimental data. This observation is traced back to an enhanced turbulent mixing by turbulent dispersion being present for the SAS that contributes to a more homogeneous field of characteristic droplet sizes in the tank.
In Figure 3, the 𝑑̅32 field for both turbulence models is depicted. For the SST results, large blurred structures are identifiable in Figure 3a). In contrast, smaller scale turbulent fluctuations resolved by the SAS model are clearly visible in Figure 3b). Hence, on the one hand, the spatial variation of the 𝑑̅32 field is significantly narrower for the SAS, leading to a more homogeneous field of droplet sizes throughout the tank and especially at the measurement locations ML-I and
ML-T, which is in line with the experimental observations. On the other hand, there is some evidence from experiments that the TEDR might be underestimated by the SAS model. Although this effect may be compensated by a recalibration of kernel parameters, further studies are planned to enhance the prediction of the TEDR.
Discussion
𝐴𝑑𝑖𝑠 = 0.05.
Refrences
[1] Issa, R. I. (1986). Solution of the implicitly discretised fluid flow equations by operator-splitting. Journal of Computational Physics, 62(1), 40–65. DOI: 10.1016/0021-9991(86)90099-9.
[2] Jasak, H. (1996). Error Analysis and Estimation for the Finite Volume Method With Applications to Fluid Flows. Ph.D. thesis, Imperial College of Science, Technology and Medicine, London.
[3] Hundshagen, M., Rave, K., Nguyen, B., Popp, S., Hasse, C., Mansour, M., Thevenin, D., Skoda, R. (2022). Two-Phase Flow Simulations of Liquid/Gas Transport in Radial Centrifugal Pumps with Special Emphasis On the Transition From Bubbles to Adherent Gas Accumulations. ASME Journal of Fluids Engineering, 144(10), 101202. DOI: 10.1115/1.4054264.
[4] Rave, K., Hermes, M., Wirz, D., Hundshagen, M., Friebel, A., von Harbou, E., Bart, H.-J., Skoda, R. (2022). Experiments and fully transient coupled CFD-PBM 3D flow simulations of disperse liquid-liquid flow in a baffled stirred tank. Chemical Engineering Science, 253, 117518. DOI: 10.1016/j.ces.2022.117518.
[5] Rave, K., Hermes, M., Hundshagen, M., Skoda, R. (2023). Assessment of scale-adaptive turbulence modeling in coupled CFD-PBM 3D flow simulations of disperse liquid-liquid flow in a baffled stirred tank with particular emphasis on the dissipation rate. Chemical Engineering Science, 270, 118509. DOI: 10.1016/j.ces.2023.118509.
[6] Egorov, Y., Menter, F. R. (2008). Development and Application of SST-SAS Turbulence Model in the DESIDER Project. In: Peng, S.-H., Haase, W. (Eds.), Advances in Hybrid RANS-LES Modelling. Springer, Berlin, Heidelberg, 261–270. DOI: 10.1007/978-3-540-77815-8_27.
[7] Menter, F. R. (1994). Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal, 32(8), 1598–1605. DOI: 10.2514/3.12149.
[8] Coulaloglou, C., Tavlarides, L. (1977). Description of interaction processes in agitated liquid-liquid dispersions. Chemical Engineering Science, 32(11), 1289–1297. DOI: 10.1016/0009-2509(77)85023-9.
[9] Hsia, M., Tavlarides, L. (1983). Simulation analysis of drop breakage, coalescence and micromixing in liquid-liquid stirred tanks. Chemical Engineering Journal, 26(3), 189–199. DOI: 10.1016/0300-9467(83)80014-8.
Additional Project Information
DFG classification: 404-03 Fluid Mechanics
Software: OpenFOAM
Cluster: CLAIX
Publications
Rave, K., Hermes, M., Hundshagen, M., Skoda, R. (2023). Assessment of scale-adaptive turbulence modeling in coupled CFD-PBM 3D flow simulations of disperse liquid-liquid flow in a baffled stirred tank with particular emphasis on the dissipation rate. Chemical Engineering Science, 270, 118509. DOI: 10.1016/j.ces.2023.118509.
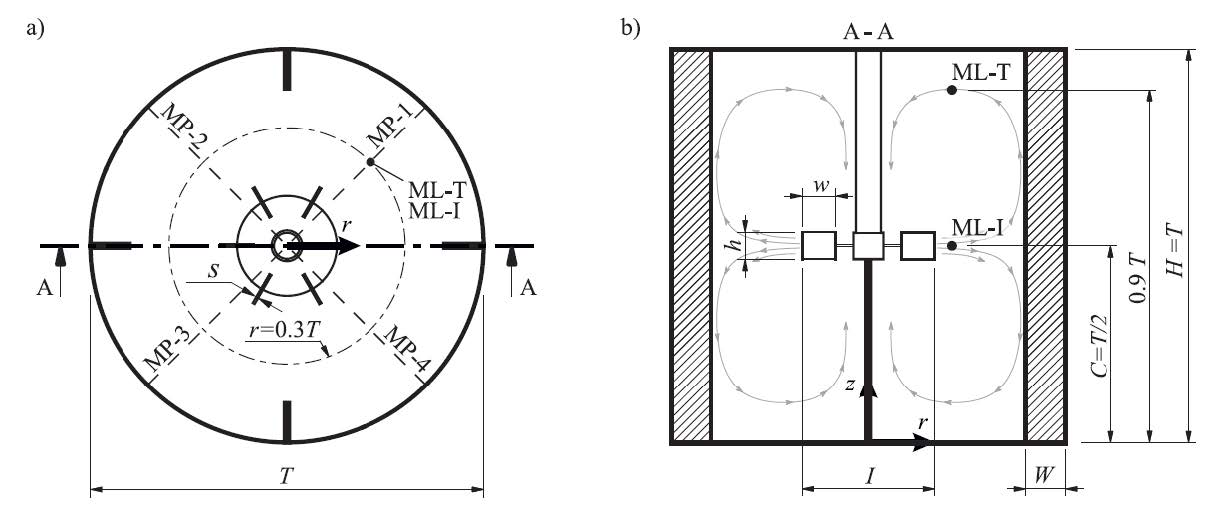 Figure 1: a) Top view and b) sectional view of the stirred tank. The measurement locations ML-T and ML-I are marked. The Figure is adopted from [5].
Figure 1: a) Top view and b) sectional view of the stirred tank. The measurement locations ML-T and ML-I are marked. The Figure is adopted from [5]. 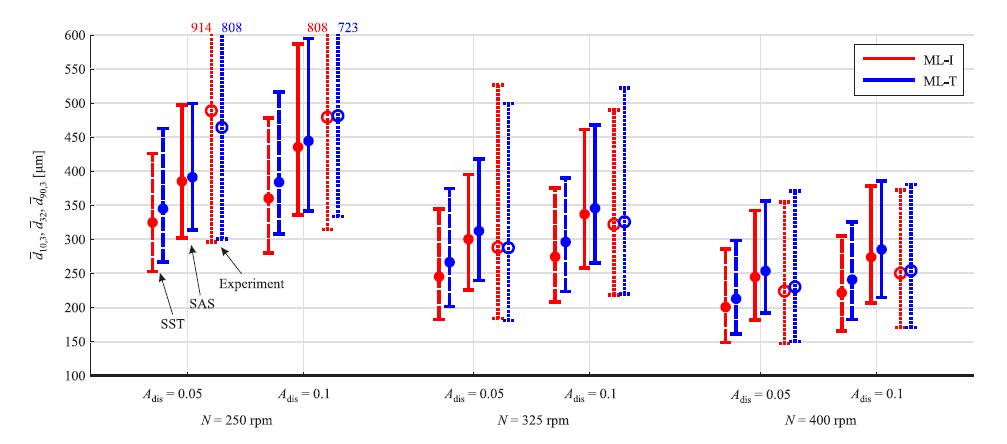 Figure 2: Time-averaged DSDs in terms of 𝑑̅10,3, 𝑑̅32 and 𝑑̅90,3 for a variation of the operating point. Simulations have been performed on a grid comprising the full 360° domain and consisting of 3.1 million cells. The Figure is adopted from [5].
Figure 2: Time-averaged DSDs in terms of 𝑑̅10,3, 𝑑̅32 and 𝑑̅90,3 for a variation of the operating point. Simulations have been performed on a grid comprising the full 360° domain and consisting of 3.1 million cells. The Figure is adopted from [5]. 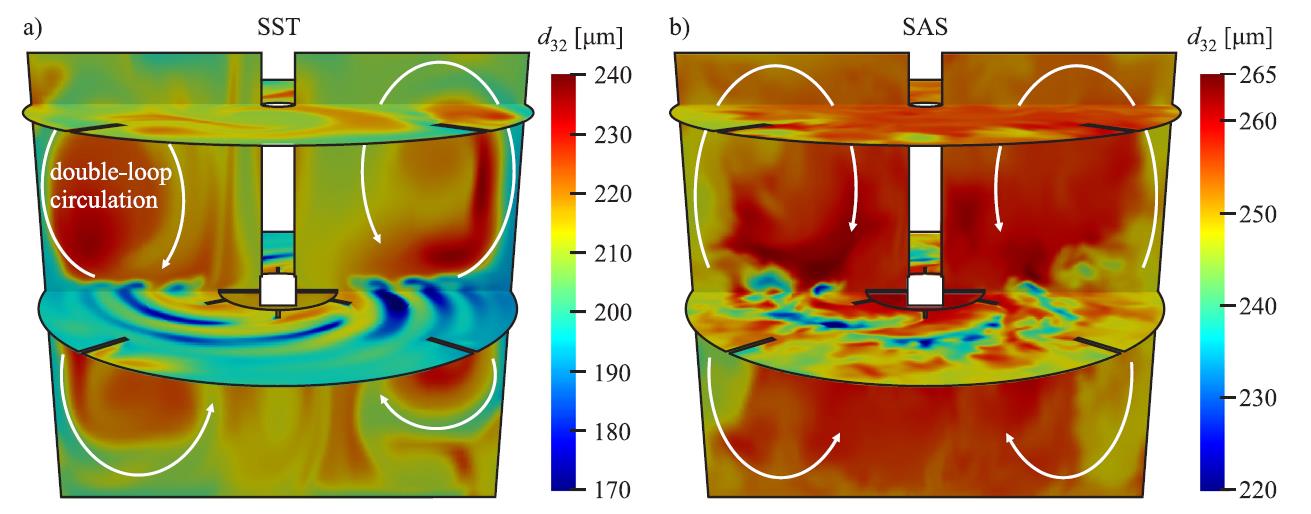 Figure 3: Instantaneous snap shots of the Sauter mean diameter 𝑑32 field obtained from a) SST model and b) SAS results after 270 impeller revolutions. Operating point is 𝑁 = 400 [rpm] and 𝐴𝑑𝑖𝑠 = 0.05. The Figure is adopted from [5].
Figure 3: Instantaneous snap shots of the Sauter mean diameter 𝑑32 field obtained from a) SST model and b) SAS results after 270 impeller revolutions. Operating point is 𝑁 = 400 [rpm] and 𝐴𝑑𝑖𝑠 = 0.05. The Figure is adopted from [5].