Project
Error Correction in Non-equilibrium Many-Body Quantum Spin Systems
Understanding and controlling the dynamics of open many-body quantum systems is both of fundamental importance to understand basic processes in nature, as well as of practical relevance in the field of quantum technology. Our research in theoretical quantum technology is mainly centred around scalable quantum computation and quantum simulation, with a focus on the development of implementations in atomic, molecular and optical systems. In this project, our overall aim is to investigate new types of non-equilibrium phases and phase transitions in open many-body quantum systems, and to explore their potential for quantum error correction, information storage, and fault-tolerant quantum computing. The computational effort accompanying these goals goes significantly beyond capacities of personal laptops or desktop computers – realising these simulations in parallel on the CLAIX HPC facility allows us to study these systems (i) in a reasonable amount of time, reaching (ii) the required simulated system sizes and (iii) statistical accuracy needed to quantitatively characterise the novel physics of these systems.
Project Details
Project term
February 1, 2022–January 31, 2023
Affiliations
RWTH Aachen University
Forschungszentrum Jülich
Institute
Institute for Theoretical Nanoelectronics
Project Manager
Principal Investigator
Methods
We use the following numerical methods, which we adapt to the specific physical models and questions. To develop a qualitative understanding of the physics of the considered models and to benchmark numerical code we perform exact density matrix simulations of open quantum systems. To this end we employ an open-source software called Qutip, which is a Python framework for simulating quantum systems and allowing us to perform simulations for small systems of up to about ten qubits. To simulate the approximate time-evolution of open quantum systems, we use the quantum trajectories approach. This method describes the dynamics of a system via the evolution of individual pure state wavefunctions of many-body quantum systems being prone to open systems quantum jumps. Upon performing the ensemble average of these trajectories, the time evolved density matrix can be determined. Furthermore a tensor network based method, the so-called density matrix renormalisation group approach is employed. So-called matrix product states are used to represent quantum many-body states. It relies on the possibility to truncate the Hilbert space by reducing the rank of all matrices to a maximum value, referred to as “bond dimension”, but keeping it large enough to approximate its physics correctly.
In order to characterize noisy quantum error correcting circuits and codes, the python package “PECOS” is used. It allows for both stabilizer and wavefunction simulations, being able to define realistic error models for faulty quantum operations. For stabilizer simulations, one can simulate large system sizes efficiently, allowing to assess e.g. scaling of logical error rates for topological quantum error correcting codes with increasing qubit register sizes. On the other hand, wavefunction simulations are limited to a dozens of qubits, but allow for the incorporation of arbitrary noise models and therefore realistic modelling of state-of-the-art experimental quantum processors. For both types of simulations, one has to average over large number of QEC trajectories, for different noise realisations, to obtain statistically reliable predictions of QEC code performance. Thus, Monte Carlo sampling makes up a substantial part of our numerical effort.
Results
We have successfully completed the study on measurement-induced transitions and established a connection to active quantum error correction protocols. A paper containing those results is in preparation for peer-reviewed publication. Furthermore, we investigated the associative memory behaviour of the multi-mode Dicke model in the low pattern storage regime. This was done analytically and via numerical simulations based on Monte Carlo techniques. Moreover, we worked on a quantum Hopfield generalisation to study the maximal storage capacity of a quantum Hopfield network. To map out the maximal capacity we solved a set of self-consistent meanfield equations numerically – a manuscript containing the results is accepted as a peer-reviewed publication in the journal Physical Review Research. Using the Matrix product state approach, we were able to simulate relatively large systems while keeping the computational resources low. Complementary, we used these exact diagonalisation techniques based on tensor network states for the determination of ground states of the Mott insulating systems. The results are
published as a preprint. We performed extensive numerical Monte Carlo simulations in order to assist the experimental breakthrough realisation of a fault-tolerant universal gate set on a trapped ion architecture. Furthermore, we developed fault tolerant protocols for code switching between the 2D and 3D color codes (master’s thesis and paper in preparation F. Butt et al.), for the correction of qubit loss in planar color codes (master’s thesis D. Scheer) and further investigated the interpretability of neural network decoders (master’s thesis and paper in preparation L. Kusters et al.).
Discussion
We have finalised our study on measurement-induced transitions having obtained valuable insights for the field of quantum error correction. Upon changing the research focus of this subproject, we plan to explore in the future (i) topological quantum phases in cold atomic quantum simulators, and (ii) robust quantum simulation protocols for quantum lattice gauge theories. With regard to our work on open quantum associative networks we plan to extend our capacity analysis towards cavity models for experimental implementations of a quantum Hopfield model and models that allow for information storage in coherent subspaces. Finally, building on our advances with respect to active error correction protocols, we aim to develop and simulate new fault protocols that are relevant in near term experiments. In particular we will work on quantum Low Density Parity Check codes to develop new QEC codes with interesting properties such as a finite ratioof encoded to physical qubits.
Additional Project Information
DFG classification: 308 Optics, Quantum Optics and Physics of Atoms, Molecules and Plasmas
Software: Matlab, Mathematica
Cluster: CLAIX
Publications
Lukas Bödeker, Eliana Fiorelli, Markus Müller. Optimal storage capacity of quantum Hopfield neural networks, arXiv [2210.07894], 2022.
Sergi Julià-Farré, Lorenzo Cardarelli, Maciej Lewenstein, Markus Müller, Alexandre Dauphin, Topological stripe state in an extended Fermi-Hubbard model, arXiv [2301.03312], 2023.
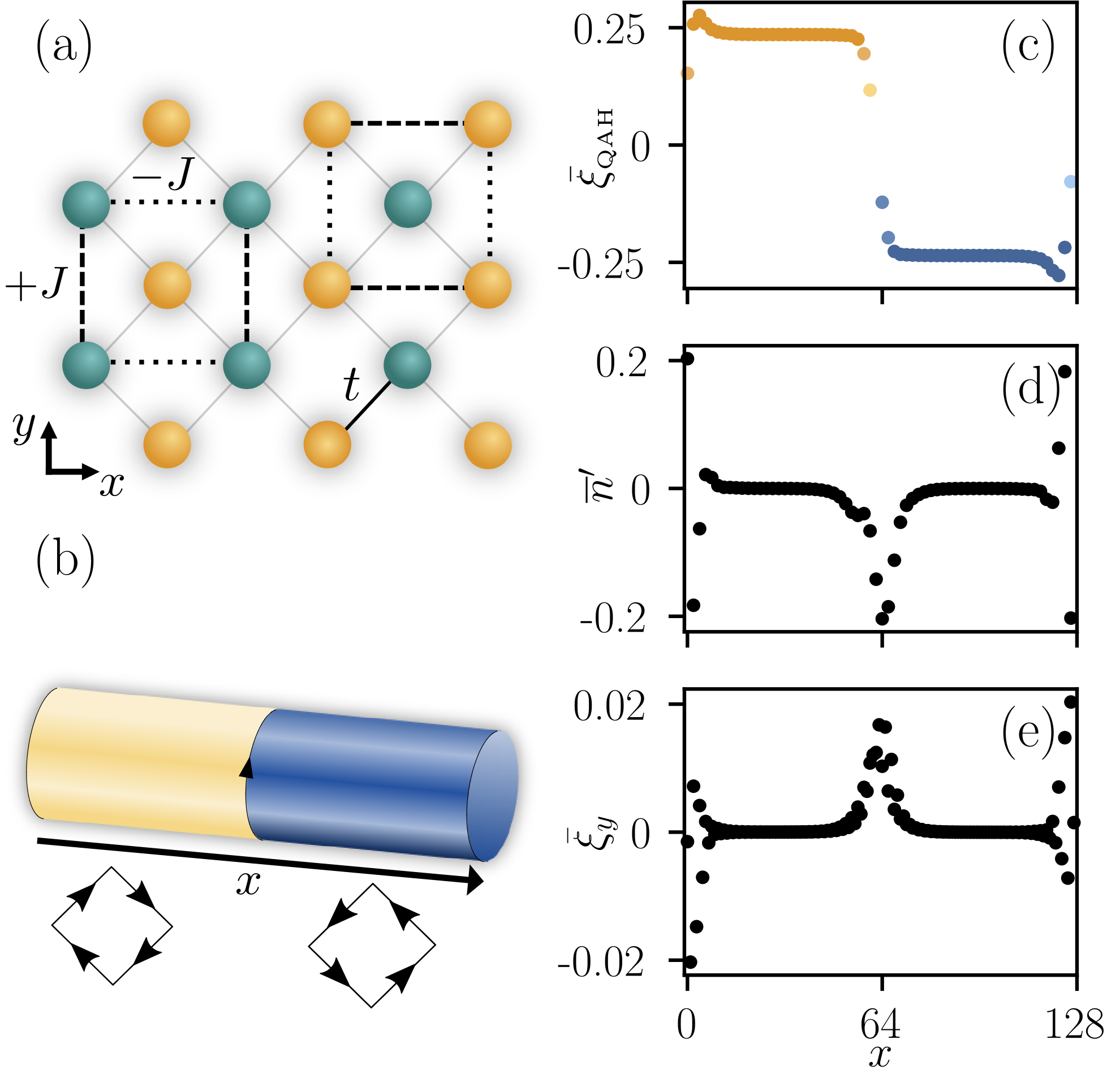 Figure 1: Schematics of an interacting model of fermions on a checkerboard lattice (a)
hosting a topological stripe state in a cylinder geometry (b). Topological order
parameter and density profile (right).
Figure 1: Schematics of an interacting model of fermions on a checkerboard lattice (a)
hosting a topological stripe state in a cylinder geometry (b). Topological order
parameter and density profile (right). 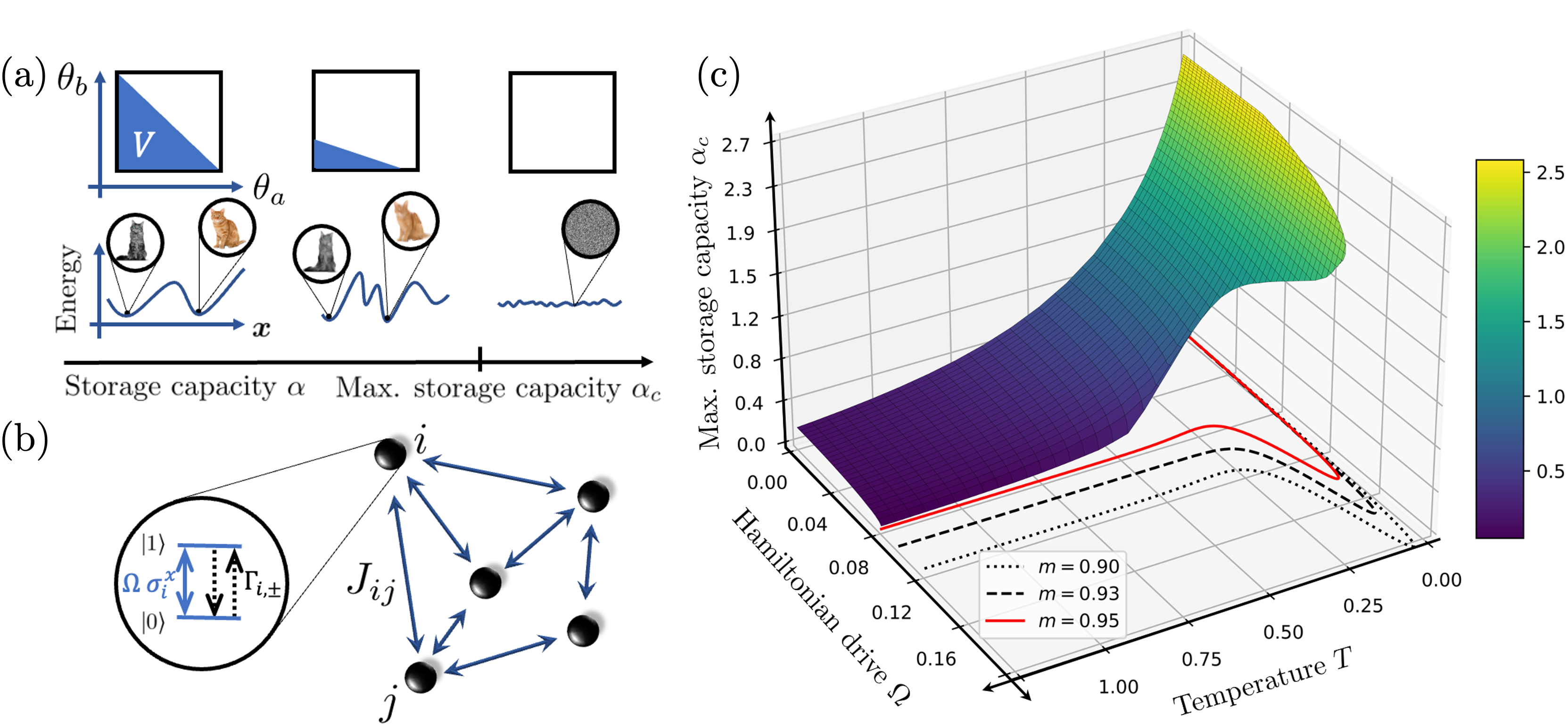 Figure 2: Schematics of a pattern storage in quantum neural networks. (a) Upon increasing the number of stored patterns, the volume of parameters where pattern retrieval is possible shrinks, until reaching a critical threshold. (b) Schematics of an open quantum Hopfield neural network of interacting spin-1/2 particles. (c) Maximal storage capacity of the quantum neural network as a function of adversary temperature and Hamiltonian perturbation effects.
Figure 2: Schematics of a pattern storage in quantum neural networks. (a) Upon increasing the number of stored patterns, the volume of parameters where pattern retrieval is possible shrinks, until reaching a critical threshold. (b) Schematics of an open quantum Hopfield neural network of interacting spin-1/2 particles. (c) Maximal storage capacity of the quantum neural network as a function of adversary temperature and Hamiltonian perturbation effects.