Project
Error correction in non-equilibrium many-body quantum spin systems
Understanding and controlling the dynamics of open many-body quantum systems is both of fundamental importance for understanding basic processes in nature and of practical relevance in the field of quantum technology. Our research has led to new protocols for the quantum simulation of closed and open many-body systems, the theoretical development of quantum mechanical neural networks, and the design and study of quantum error correction protocols for fault-tolerant quantum computation. These efforts have in several cases resulted in experimental realizations that have been supported by us in terms of providing theory proposals as well as by numerical simulations. In this project, our overall aim was to investigate open many-body quantum systems and explore their potential for quantum error correction, information storage, and fault tolerant quantum computing. The project is divided into three sub-projects: First, we aimed to investigate atomic, molecular, and optical (AMO) systems for quantum simulation and computation purposes. Second, we studied how quantum-mechanical effects can impact the performance of neural networks, in particular with regard to (potentially increased) information storage capabilities, by determining the storage capacity of quantum generalizations of the Hopfield model. Third, we identified the parameter regimes for beneficial fault-tolerant quantum error correction (QEC) based on topological quantum codes. The computational effort accompanying these goals goes significantly beyond capacities of personal laptops or desktop computers – realising these simulations in parallel on the CLAIX HPC facility allows us to study these systems (i) in a reasonable amount of time, reaching (ii) the required simulated system sizes and (iii) statistical accuracy needed to quantitatively characterize the novel physics of these systems.
Project Details
Project term
February 1, 2024–March 1, 2025
Affiliations
RWTH Aachen University
Institute
Institute for Quantum Information
Principal Investigator
Methods
In order to develop a qualitative understanding of the physics of the considered models and to benchmark our code, we perform exact density-matrix simulations of open quantum systems using the open-source Python framework QuTiP, which supports systems of up to about ten qubits. For approximate time evolution, we employ the quantum
trajectories approach, simulating many pure-state evolutions with stochastic quantum jumps and averaging them to obtain the density matrix. We also use a tensor-network method — the density matrix renormalization group — representing many-body states as matrix product states. By truncating matrix ranks to a chosen “bond dimension,” we reduce the Hilbert space while retaining the essential physics. For noisy quantum error correction (QEC) circuits, we use PECOS and Stim, which allow separate specification of circuits and error models. Clifford circuits with Pauli noise are simulated using the efficient stabiliser simulators. For arbitrary noise models relevant to realistic hardware, we run state-vector simulations via ProjectQ as a backend to PECOS. Logical error rates and other metrics are estimated by Monte Carlo sampling over 103-105 trajectories per parameter set on CPU clusters, ensuring statistically reliable results.
Results
This project focuses on non-equilibrium behavior in open many-body quantum systems and how novel phenomena can enable quantum error correction. In this context, our group has already achieved several notable results. We developed and applied a new simulation technique called dynamical subset-sampling that efficiently handles non-deterministic fault-tolerant protocols while greatly reducing computational cost [1]. We also explored quantum cellular automata as a route to autonomous error correction, translating classical local update rules into dissipative quantum circuit operations [5]. On the side of designing new quantum error correcting codes, we introduced lift-connected surface codes, a new family of low-density parity-check codes with improved performance over standard surface codes at moderate qubit counts [3]. Together with collaborators, we conceived the XYZ ruby code, a time-dependent error correction code described through a tensor-network graphical calculus, and analyzed its performance under realistic noise [7]. Inspired by developments in hardware, we carried out studies on optimized stabilizer readout using three-qubit gates for superconducting and ion-trap platforms [11], and assessed how moving spin qubits between locations affects the reliability of a surface code memory [12]. We also proposed a fully measurement-free fault-tolerant error correction scheme for systems where fast intermediate measurements are not possible, identifying realistic operating conditions for both neutral atoms and trapped ions [2]. Our group contributed to major experimental milestones, including the first demonstration in trapped ions of switching between two different error correction codes during a computation, enabling a complete set of logical operations [6], published in the high impact journal Nature Physics. Beyond error correction, we advanced the study of open many-body quantum systems relevant to quantum technologies. This included the development of a noise-aware variational optimization method for preparing the lowest-energy state of the Z2 lattice gauge theory [4], achieving high accuracy with circuits short enough to run on current devices.
Discussion
As discussed above, over the past two years, we have advanced both the theory and practical feasibility of fault-tolerant quantum error correction, introducing new code families, efficient simulation methods, and hardware-tailored protocols. Several developments were tested through experimental collaborations, highlighting the close link between our modelling and real-world implementations. In the next year, we will focus on three main directions. First, we will design and optimize native multi-qubit gates for Rydberg atoms and ions, requiring large-scale numerical optimization of pulse sequences. Second, we will expand our use of classical and quantum neural networks for error correction, aiming to improve decoding performance and explore autonomous correction in lattice models. Third, we will benchmark fault-tolerant protocols in specific hardware settings, including surface code readout with multi-qubit gates, qubit shuttling in spin and ion-trap platforms, and protocols for magic-state distillation and injection. These efforts will strengthen the bridge between theoretical design and experimental capability, supporting progress towards scalable, fault-tolerant quantum computation.
Additional Project Information
DFG classification: 308 Optics, Quantum Optics and Physics of Atoms, Molecules and Plasmas
Software: Python3, Matlab, Mathematica
Cluster: CLAIX
Publications
1. Sascha Heußen, Don Winter, Manuel Rispler, and Markus Müller, “Dynamical subset sampling of quantum error-correcting protocols,” Phys. Rev. Research, 2024, 6, 013177.
2. Sascha Heußen, David F. Locher, and Markus Müller, “Measurement-free fault tolerant quantum error correction in near-term devices,” PRX Quantum, 2024, 5, 010333.
3. Josias Old, Manuel Rispler, and Markus Müller, “Lift-connected surface codes,” Quantum Sci. Technol., 2024, 9, 045012.
4. Jesús Cobos, David F. Locher, Alejandro Bermudez, Markus Müller, and Enrique Rico, “Noise-aware variational eigensolvers: a dissipative route for lattice gauge theories,” PRX Quantum, 2024, 5, 030340.
5. Thiago L. M. Guedes, Don Winter, and Markus Müller, “Quantum cellular automata for quantum error correction and density classification,” Phys. Rev. Lett., 2024, 133, 150601.
6. Ivan Pogorelov, Friederike Butt, Lukas Postler, Christian D. Marciniak, Philipp Schindler, Markus Müller, and Thomas Monz, “Experimental fault-tolerant code switching,” Nat. Phys., 2025, 21, 298–303.
7. Julio C. Magdalena de la Fuente, Josias Old, Alex Townsend-Teague, Manuel Rispler, Jens Eisert, and Markus Müller, “XYZ ruby code: making a case for a three-colored graphical calculus for quantum error correction in spacetime,”
PRX Quantum, 2025, 6, 010360.
8. Joseph W. P. Wilkinson, Katrin Bolsmann, Thiago L. M. Guedes, Markus Müller, and Igor Lesanovsky, “Two-qubit gate protocols with microwave-dressed Rydberg ions in a linear Paul trap,” New J. Phys., 2025, 27, 064502.
9. Thomas Botzung, Michael Buchhold, Sebastian Diehl, and Markus Müller, “Robustness and measurement-induced percolation of the surface code,” J. Phys. A: Math. Theor., 2025, 58, 205304.
10. Lukas Bödeker, Luc J. B. Kusters, and Markus Müller, “On the interpretability of neural network decoders,”
Adv. Quantum Technol., 2025, 8, e2500158.
11. Josias Old, Stephan Tasler, Michael J. Hartmann, Markus Müller, “Fault-Tolerant Stabilizer Measurements in Surface Codes with Three-Qubit Gates“, arXiv, 2025.
12. Berat Yenilen, Arnau Sala, Hendrik Bluhm, Markus Müller, Manuel Rispler, “Performance of the spin qubit shuttling architecture for a surface code implementation“, arXiv, 2025.
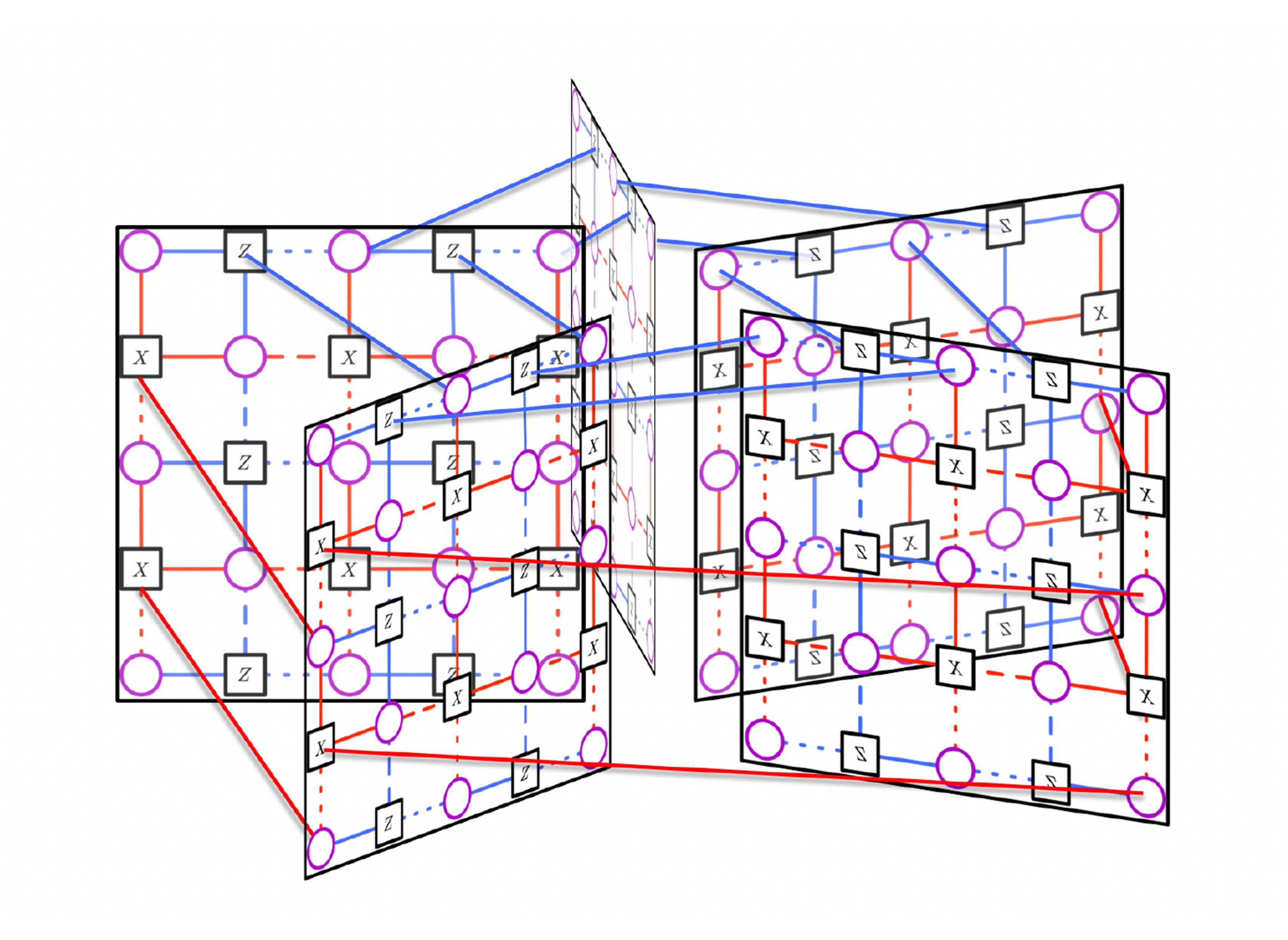 Figure 1: Possible arrangement of qubits of the [[65, 5, 5]](2,5) LCS code, corresponding to 5 interconnected [[13, 1, 3]] surface codes. While only a few interconnections of the patches are shown, note that all connectivity is restricted to neighbors of neighboring patches and therefore 3D-local.
Figure 1: Possible arrangement of qubits of the [[65, 5, 5]](2,5) LCS code, corresponding to 5 interconnected [[13, 1, 3]] surface codes. While only a few interconnections of the patches are shown, note that all connectivity is restricted to neighbors of neighboring patches and therefore 3D-local.  Figure 2: Logic rule of two cellular automata (a,c). Quantum-circuit representations of the QCA (d,e,h,i). Schematics of an implementation with Rydberg atoms (b). Exemplary executions of the QCA (f,j,k).
Figure 2: Logic rule of two cellular automata (a,c). Quantum-circuit representations of the QCA (d,e,h,i). Schematics of an implementation with Rydberg atoms (b). Exemplary executions of the QCA (f,j,k).