Project
Analysis of Aerodynamic Noise Generation and Propagation in a Centrifugal Compressor
Radial compressors are one of the main sources of noise in most plants they are part of. Due to the decentralization of such plants as part of the energy transition and the growing social awareness of the negative health consequences of noise pollution, the sound emissions of radial compressors are increasingly becoming the focus of research. In this project, the sound generation mechanisms of radial compressor with vaned diffusers were numerically analyzed for multiple operating points. Due to the required size of the computational grid, the unsteady simulations require HPC resources.
Project Details
Project term
January 1, 2021–December 31, 2021
Affiliations
RWTH Aachen University
Institute
Institute of Jet Propulsion and Turbomachinery
Principal Investigator
Methods
In this computing project, the sound generation and propagation within a radial compressor were modeled using URANS simulations. In order to simulate the acoustic phenomena, high spatial and temporal resolutions are needed. For the spatial resolution, 30 grid points per wavelength was targeted resulting in maximum cell size of approx. 1.3 mm. The temporal resolution was set to 128 time steps per period, i.e. 1792 time steps per revolution, following a time step study. The turbulence was modeled with the k-ω turbulence model of Wilcox. A similar numerical setup was already used in previous projects resulting in satisfactory agreement with experimental data.
Results
The sound generation mechanisms of the considered radial compressor were analyzed for two operating points, the aerodynamic design point of the impeller (OP2) and an operating point close to the choke limit (OP1). For radial compressors of this size, the tonal components dominate the sound emissions and broadband components are negligible. In radial compressors with vaned diffusers, the impeller-diffuser interaction is the main source of tonal sound. For this reason, the analyses focused on the diffuser.
The results of the unsteady simulations were given by the flow properties, e.g. pressure and Mach number, at an instantaneous time step and their temporal Fourier Transformation over one period (equal to one blade passing). Figure 1 shows the pressure fluctuations at an instantaneous time step for the first blade passing frequency at 10% diffuser height for OP2. At the marked diameters at the diffuser inlet and diffuser outlet, a spatial Discrete Fourier Transformation of the complex pressure from the Fourier results were performed to obtain the azimuthal mode spectrum of the pressure fluctuations. These pressure fluctuations include the acoustic fluctuations as well as the convective ones. In Figure 1, the dominant modes are marked by the position of their pressure maxima at the depicted time step. The pressure amplitudes of all modes of the first and second blade passing frequency (BPF1 & BPF2) are shown in Figure 2 at the diffuser inlet (left) and diffuser outlet (right) for OP2. At the diffuser inlet, there are two clearly dominant modes at BPF1 as well as at BPF2. The mode orders 𝑚𝐵𝑃𝐹1 = 14 and 𝑚𝐵𝑃𝐹2 = 28 correlate to the number of impeller blades and are excited by the wakes of the blunt trailing edges. The mode orders 𝑚𝐵𝑃𝐹1 = 5 and 𝑚𝐵𝑃𝐹2 = 19 are caused by the interaction of these wakes with the diffuser vanes. These modes are called Tyler-Sofrin-modes and their mode order can be calculated by
m𝑇𝑦𝑙𝑒𝑟−𝑆𝑜𝑓𝑟𝑖𝑛 = h⋅ZImpeller − 𝑘⋅𝑍Diffuser
Here, ℎ represents the harmonic of the considered frequency, 𝑘 is any integer and 𝑍𝐼𝑚𝑝𝑒𝑙𝑙𝑒𝑟 and 𝑍𝐷𝑖𝑓𝑓𝑢𝑠𝑒𝑟 are the number of blades in the impeller and diffuser, respectively.
At the diffuser outlet, the mode spectrum is more diffuse with an additional dominant Tyler-Sofrin-mode 𝑚𝐵𝑃𝐹1 = −4 at BPF1. At BPF2, the mode order 𝑚𝐵𝑃𝐹2 = 28 is attenuated leaving 𝑚𝐵𝑃𝐹1 = 19 as the single dominant mode. Figure 3 shows the same pressure amplitudes as Figure 2 for an operating point near the choke limit (OP1). The azimuthal mode spectrum of OP1 at the diffuser inlet is very similar to the one of OP2 with slightly lower pressure amplitudes. However, when normalizing the pressure amplitudes with the average static pressure in these planes, the normalized pressure amplitudes are higher for all dominate modes except 𝑚𝐵𝑃𝐹1 = 5.
At the diffuser outlet, the mode 𝑚𝐵𝑃𝐹1 = 14 is clearly dominant at BPF1. In addition to the Tyler-Sofrin-modes 𝑚𝐵𝑃𝐹1 = 5 and 𝑚𝐵𝑃𝐹1 = 3, the modes 𝑚𝐵𝑃𝐹1 = 15 and 𝑚𝐵𝑃𝐹1 = 16 also have significant amplitudes at slightly above 50% of 𝑚𝐵𝑃𝐹1 = 14. These modes are excited by an interaction of the impeller wakes with the volute. The results at BPF2 are very similar to OP2 only with higher normalized amplitudes.
Discussion
In this project, the sound generation mechanisms of a radial compressor with a vaned diffuser were successfully identified at two operating points. The dominant mechanisms are the rotor-alone noise, the impeller-diffuser interaction and, in case of an operating point near choke, the impeller-volute interaction. Originally, a third operating point close to the surge limit was supposed to be included in these analyses. However, since only a third of the applied computing time was granted, this simulation could not be run until convergence. The results of these simulations will also be used in future analyses of the sound field and sound emission the discharge line downstream of the volute. Additionally, experimental acoustic measurements are planned for the considered radial compressor so that the numerical results can be validated.
Additional Project Information
DFG classification: 402-04 Acoustics
Software: TRACE
Cluster: CLAIX
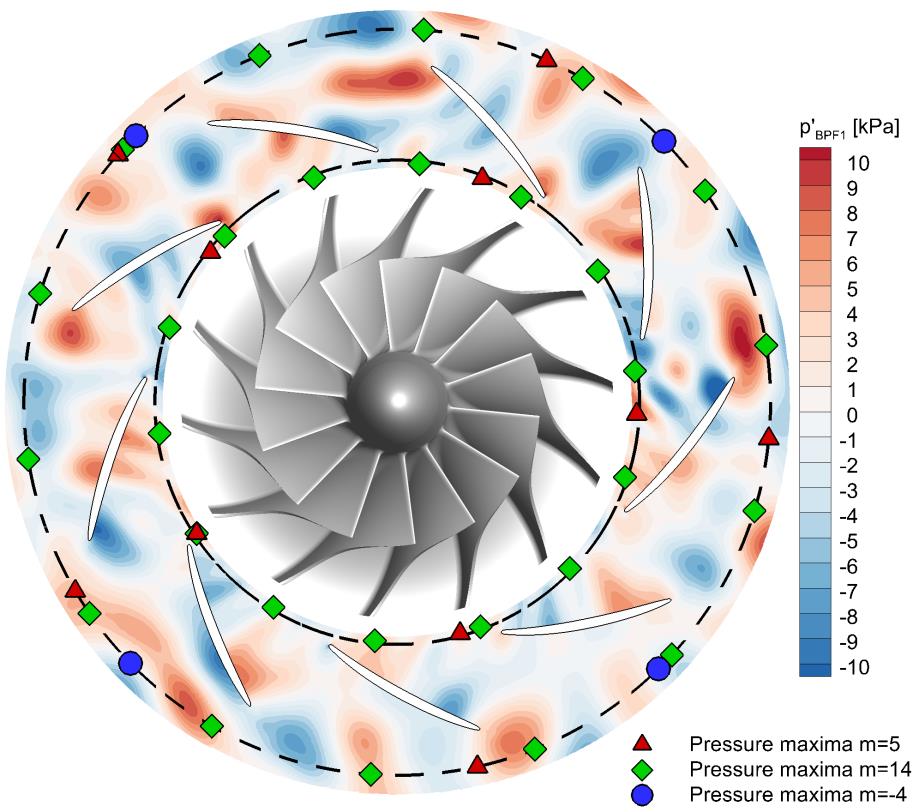 Figure 1: Instantaneous pressure fluctuations and pressure maxima of the dominant modes of the first blade passing frequency (BPF1) at the diffuser inlet and diffuser outlet for OP2.
Figure 1: Instantaneous pressure fluctuations and pressure maxima of the dominant modes of the first blade passing frequency (BPF1) at the diffuser inlet and diffuser outlet for OP2. 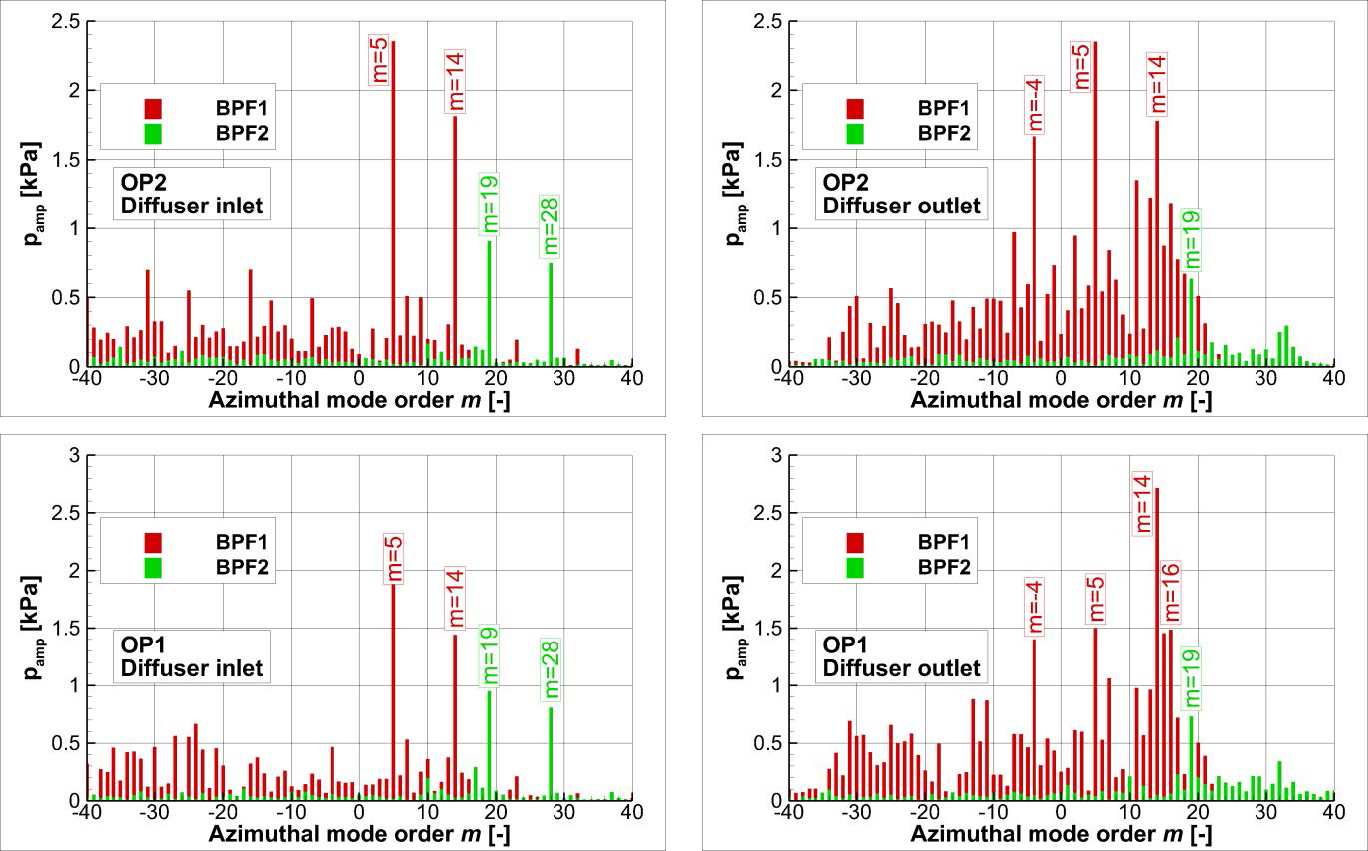 Figure 2: Pressure amplitudes of the azimuthal modes at the diffuser inlet (left) and diffuser outlet (right) of BPF1 and BPF2 for OP2.
Figure 2: Pressure amplitudes of the azimuthal modes at the diffuser inlet (left) and diffuser outlet (right) of BPF1 and BPF2 for OP2.