Project
Insights on ligand/CAG repeat RNA interactions in Huntington’s disease by metadynamics simulations
Huntington disease (HD) is an autosomal dominant disorder that leads to motor, cognitive and behavioral symptoms. It belongs to the CAG triplet repeat expansion diseases, a very important group of genetically caused neurodegenerative diseases [1]. Neuronal dysfunction associated with HD involves the human mutant HTT gene. The latter contains less than 35 CAG repeats in healthy individuals, whereas more than 40 repeats invariably cause the disease. Mutant HTT (i.e. the HTT gene with more than 40 repeats) encodes for a messenger RNA (mutCAG-RNA) that folds into a hairpin [2-5]. The hairpin abnormally captures RNAbinding proteins (such as MID1 [6]), leading to aberrant processes such as translation initiation of the mutCAG-RNA (by trapping parts of the translation machinery) and aberrant splicing (by trapping splice factors) [7-10]. Ligands interfering with mutCAG-RNA-protein interactions may provide important insight into the impact of mutCAG-RNA on the development of HD and may act as leads for therapeutic agents targeting the disease. However, identifying such ligands poses challenges to standard in silico drug design methods, such as molecular docking approaches. The latter identify putative binding pockets of biomolecules, they can predict the ligand poses onto them and, finally, they rank the reliability of the poses based on a “docking score”. However, these approaches have been developed mostly for proteins and may encounter difficulties for RNA binders, as (i) the cavities in the latter are usually shallow and solvent-exposed (unlike those of receptors and enzymes), (ii) the electrostatic potential is strongly affected by the RNA as a polyelectrolyte along with counterions, and (iii) RNAs’ high flexibility challenges the assumption that the binding pocket is a (quasi-)locked conformation of most docking approaches [11]. In addition, they provide neither quantitative binding affinities, nor the free energy landscape associated with ligand binding. All of this information can be instead obtained by enhanced sampling methods. For the last years, our group has been carrying out Well-tempered Metadynamics (WTMetaD) [12-15] free energy simulations to investigate the potency and binding poses to ligands binding to CAG repeats RNA [16,17]. One of them, furamidine, has turned out to be the first ligand able to inhibit the RNA encoding for the huntingtin protein in living cells and affect the binding of RNA hairpin cellular partners, as shown experimentally by our collaborator Sybille Krauss at the University of Siegen [17]. Unfortunately, however, furamidine is neurotoxic; therefore, there is a necessity of improvement through searching for further RNA-binding candidates with high affinity and no toxicity. Here we planned to use classical molecular dynamics, as well as WTMetaD simulations, to predict pose and free energy of binding of RNA ligands in explicit solvent. We focused on one of the complexes of ligand binding to RNA with CAG triplet repeat expansion whose NMR structures are available [18]. In this complex, the RNA (CAG RNA hereafter) forms a hairpin structure and the ligand
N’-{(Z)-amino[4-(amino{[3-(dimethylammonio)propyl]iminio methyl)phenyl]methylidene}-N,N-dimethylpropane-1,3-diaminium (DB213) binds to the major groove of CAG RNA (Fig. 1).
Project Details
Project term
April 1, 2024–April 1, 2025
Affiliations
RWTH Aachen University
Institute
I. Physikalisches Institut B
Principal Investigator
Methods
System preparation
Among the ensemble of five NMR structures of the CAG RNA-DB213 complex, (PDBid 7D12) [18], we chose the first conformer as the starting structure for our study. We also ran additional simulations (classical MD and QM/MM) on a system consisting of only the ligand in water. Preparation steps for the two systems: (A) CAG RNA-DB213 complex in water: The simulation box is an 8.7×8.7×8.7 nm cubic box, in which the shortest distance from the complex to the edges of the box was set to 2.2nm to avoid self-interactions with periodic images. The complex was placed in the center of the box and solvated with water. To neutralize the system and mimic the experimental ion concentration (35mM NaCl), 29 Na+ and 14 Cl– ions were added to the system. (B) DB213 ligand in water: The ligand was solvated in an 8.4×8.4×8.4 cubic box of water. 12 Na+ and 16 Cl– ions were added to neutralize and give the system the ionic conditions as the CAG RNA-DB213 complex.
Molecular Dynamics
We tested two sets of force field parameters to describe CAG RNA, water and ions. The first is AMBER-parmbsc0 force field [19] for RNA, TIP3P [20] for water and Joung-Cheatham [21] parameters for ions. We referred to this set as the AMBER force field. The second set is the new force field parameters for RNA/DNA developed and revised by the D. E. Shaw Research group (New York, United States) named DES-Amber [22]. In this force field, they parameterized the ions in different ways, and used the TIP4P-D model to describe water. We referred to this set as the DES-Amber force field. For the ligand parameterization, the partial atomic charges of the ligands were the RESP charges [23] from ab initio calculation (by Gaussian 09 package [24]) of ligand in vacuum, using B3LYP functional and 6-31G(d,p) basis sets. The other parameters were given by General AMBER Force Field (GAFF) [25]. We ran MD simulations to study the dynamics of the complex using AMBER and DESAmber force fields. All the force field-based MD simulations were performed using GROMACS/2021.7 [26]. LINCS algorithm [27] was used to constraint all bonds to hydrogen atoms. The cut-off for short-range electrostatic interactions and van der Waals was set to 12 Å. The long range electrostatic interactions were treated by Particle Mesh Ewald method [28,29] with the grid spacing value of 1.2 Å. To control the temperature and pressure of the system, the Nose-Hoover thermostat [30] (time constant 0.5 ps) and isotropic Parrinello−Rahman barostat [31] (time constant 5 ps and reference pressure 1 bar) were used for the CAG RNA-DB213 complex; while the velocity rescaling with a stochastic term thermostat [32] (time constant of 0.1 ps) and the isotropic Berendsen barostat [33] ( time constant of 2 ps) was applied for the system of ligand DB213 in water. For the CAG RNA-DB213 complex, firstly, we used steepest descent [34] and conjugate gradient [35] algorithms to minimize the energy of the system (maximum force convergence criteria of 24kcalmol−1nm−1). Then the system was gradually heated to 298 K in 4ns, with harmonic restraints (spring constant of 240 kcal mol−1nm−2) applied on the heavy atoms. Next, the system was equilibrated for 1ns by NVT at 298 K, followed by 1ns NPT MD at the same temperature and at pressure 1 bar. We kept the harmonic restraints during these equilibration phases. We performed two 1 microsecond-long production run on the CAG RNA-DB213 system, one described by AMBER and one by DES-Amber force field. The restraints were released in this production phase. For the system of ligand DB213 in water, after the same energy minimization process as the complex, a 1 ns-long NPT equilibration was carried out to heat up and equilibrate the system at the same temperature and pressure (298K, 1 bar). Production run is not needed for this system.
Metadynamics
Well-tempered Metadynamics (WTMetaD) simulations [12-15] were performed only for CAG RNA-DB213 system to investigate the free energy surface of the ligand binding (as a function of appropriate collective variables – CVs) in order to identify binding poses as well as binding affinity of the ligand. Since the DES-Amber force field did not describe the system well (see Results, classical MD section), here we used the AMBER force field. A snapshot from the stable phase of the MD production was used as the starting structures for the WTMetaD simulations. Finding the suitable CVs is always a challenging task in Well-tempered Metadynamics, especially for the very complex system as the ones we studied. Therefore, we tried different sets of CVs (and also setups for the bias) on this system.
- (1 CV) Distance between the ligand center of mass and RNA center of mass
- (1 CV) Coordination number between ligand and CAG RNA
- (2 CV) Distance between the ligand center of mass and RNA center of mass + Coordination number between ligand and CAG RNA
- (2 CV) Distance between the ligand center of mass and RNA center of mass + Number of hydrophobic contacts between ligand and CAG RNA
- (2 CV) Distance between the ligand center of mass and RNA center of mass + Number of hydrogen bonds between ligand and CAG RNA
Among these sets, only the last combination (distance between the ligand center of mass and RNA center of mass and number of hydrogen bonds between ligand and CAG RNA) could reach the convergence (at 3.9 μs). In this simulation, for the bias potential, the Gaussian hills initial height was set to 0.239 kcal/mol and the Gaussian widths were set to 1 Å and 0.5 for distance and number of hydrogen bonds, respectively. The deposited rate was to 1 ps and the bias factor was 10. After the convergence, the free energy landscape as a function of the CVs was obtained from the reweighting procedure using the Tiwary-Parrinello estimator [36] on the last 1200 ns of the simulation.
QM/MM MD
QM/MM MD simulations were not performed on CLAIX-2023. The computing resources on CLAIX-2023 were instead used to conduct NMR chemical shifts calculations on QM/MM MD trajectories. Here we reported very briefly the procedure of QM/MM MD simulations. The details can be found in our published paper (see section 1.6). We performed QM/MM MD simulations on both the ligand in complex with CAG RNA and the ligand in water systems, using the last snapshots from the equilibration phase of classical MD simulations as the starting structures. The ligand (60 atoms) is described at QM level (BLYP [37,38]) and the system (including CAG RNA, water and ions) are described at MM level keeping the same force fields as the classical MD. The QM calculations were handled by the planewaves density functional theory (DFT) code CPMD [39] and the calculations for MM part were handled by GROMACS. The interactions between the QM and MM subsystems were computed by MiMiC [40]. We used Born-Oppenheimer MD with an integration timestep of ~0.24 fs. After the preparation step with MiMiCPy python package [41], simulated annealing, heating and equilibrating phase, 100 ps-long production run for the ligand-CAG RNA system and 72 ps-long production run for the ligand in water system were performed. The last 60 ps (250 snapshots) of the trajectories was used for the electronic polarization and NMR chemical shift analyses. The electronic polarization calculations were carried out by a python code, cpmd-cube-tools [42] and the NMR chemical shift calculations were carried out by ORCA program package [43,44].
Results
Classical MD
MD simulations using DES-Amber force field lead to partial or complete dissociation of the ligand (not shown) and were discarded. With AMBER force field, the ligand remained in contact with the CAG RNA during classical MD simulation. From the RMSD values of the ligand, calculated by fitting the RNA backbone to the structure after equilibration phase (starting point of production run), we saw the ligand found a stable binding pose from 200 ns to 400 ns, then the pose became more flexible (Fig. 2). Therefore, we chose the frame at 300 ns as the starting point for Metadynamics simulations.
Metadynamics
We ran WTMetaD using different sets of CVs. The simulation using two CVs consisting of (i) the distance between the ligand center of mass and RNA center of mass and (ii) number of hydrogen bonds between ligand and CAG RNA reached convergence after 3.9 μs. Unfortunately, the resulting binding poses are very different from the NMR ones and not consistent with the NOE data [18]. This suggests that the poses we obtained are not reliable. Our conclusion is that the conventional force field-based MD approach may not be accurate enough to study such a complex system. In fact, the RNA is very flexible and is highly negatively charged that can cause the polarization effect on the ligand. The fact that partial charges of each atom of the ligand are calculated on the ligand in vacuum (using ab initio RESP scheme) and kept fixed during the simulation may pose limitations in the accuracy. We therefore tried to use a more accurate approach, which includes electronic polarizability to investigate this system. This is QM/MM MD (In QM/MM description, the system is “fictitiously” partitioned into two sub-systems to be treated at different levels – QM and force field. The interaction between the QM and MM parts can be described using different schemes – subtractive scheme or additive scheme). Here, the ligand is treated at the QM level and the RNA, solvent, ions are treated at the classical level.
QM/MM MD
QM/MM MD simulations were performed on different machines, not on CLAIX-2023. The computing resources on CLAIX-2023 were only used to conduct NMR chemical shifts calculations. Here we reported very briefly the results from QM/MM MD. The details can be found in our published paper (see section 1.6). The ligand rearranges its binding pose during the QM/MM simulation, especially in the initial phase (0-40 ps). For that reason, the last 60 ps was used for analyses. In the binding pose obtained by QM/MM MD, the ligand forms more H-bonds with the CAG RNA than in the NMR structure in which we started the QM/MM simulations from (NMR1 hereafter) [18]. Indeed, in our QM/MM structure, the ligand forms three strong H-bonds instead of two weak H-bonds in NMR1 (Fig. 3). These strong H-bonds are mostly maintained he complex structure from QM/MM simulation also has stronger electrostatic interactions. Therefore, the slight changes in the binding pose of the ligand obtained from QM/MM simulation led to the improvement of the binding in term of the amount and strength of intermolecular interactions. The binding pose refined by QM/MM MD is consistent with NOE distance constraints data (120 constraints, used for NMR structure refinement) in the published NMR work [18] (see the published paper). For further verification of our structure, we also calculated the changes in 1H and 13C NMR chemical shifts of the DB213 ligand on passing from water to RNA-bound state (ppm) and compared to the experimental NMR chemical shifts (measured by the group of Martin Tollinger from University of Innsbruck, Austria). The NMR chemical shifts changes calculated for the structures obtained from the simulation are also consistent with experimental values (within the statistical errors, Tab. 1). To see the role of polarization effects of the CAG RNA on the ligand, the changes in atomic charges (ΔQ) are calculated based on changes in the electronic densities on passing from vacuum to the RNA-bound state. As expected, the largest changes occurred on hydrogen atoms (in terms of ΔQ values and the standard deviation), while the nitrogen and carbon atoms showed very minor changes (Fig. 4a). This can also be seen in the plot of the electronic density redistribution on passing from vacuum to the RNA-bound state (Figure 4b). The overall change in the charge distribution caused by polarization effects is ΔQpol = 0.2e. We concluded that the polarization effects of the RNA on the ligand are small but significant. In case of the ligand in water, the polarization effects on the ligand when passing from vacuum to water is smaller (only 0.06e). A classical MD simulation of the complex system in the same time range was performed to compare with QM/MM simulation. The MD structure could not reproduce the NOE data [18].
Discussion
We have studied the CAG RNA-DB213 ligand complex using different computational approaches. In classical MD simulations, the ligand remained in the RNA-bound state if the system is described by AMBER force field, while it left the RNA if the system is described with DES-Amber force field. The equilibrated structure from the MD simulation with AMBER force field was used as a starting point for Well-tempered Metadynamics simulations of this RNA/ligand system. The binding poses from the Metadynamics simulations were not consistent with available NOE data, possibly because of limitations of the force field used to describe RNA/ligand interactions. Therefore, we employed a more accurate approach – QM/MM MD simulations. The QM/MM MD structural ensemble shows a marked improvement in both the amount and strength of intermolecular interactions between the ligand and RNA compared to the initial structure obtained by NMR. This structure is also in good agreement with the experimental NOE data and experimental NMR chemical shifts. Due to its ability to capture electron polarization effects, QM/MM MD has an advantage in characterizing this RNA/ligand complex over classical MD. With the advent of exascale machines, QM/MM MD emerges as a useful tool to study ligand/protein interactions.
Additional Project Information
DFG classification: 310 Statistical Physics, Soft Matter, Biological Physics, Nonlinear Dynamics
Cluster: CLAIX
Publications
Hoang, G.L., Röck, M., Tancredi, A., Magauer, T., Mandelli, D., Schulz, J.B., Krauss, S., Rossetti, G., Tollinger, M. and Carloni, P.,
Refining Ligand Poses in RNA/Ligand Complexes of Pharmaceutical Relevance: A Perspective by QM/MM Simulations and NMR Measurements. The Journal of Physical Chemistry Letters, 16(7), pp.1702-1708.
Thesis:
Gia Linh Hoang, M.Sc.
Advances in predicting ligand binding poses and affinities through multiscale molecular simulations.
Faculty of Mathematics, Computer Science and Natural Sciences at RWTH Aachen University for the academic degree of Doctor of Natural Sciences
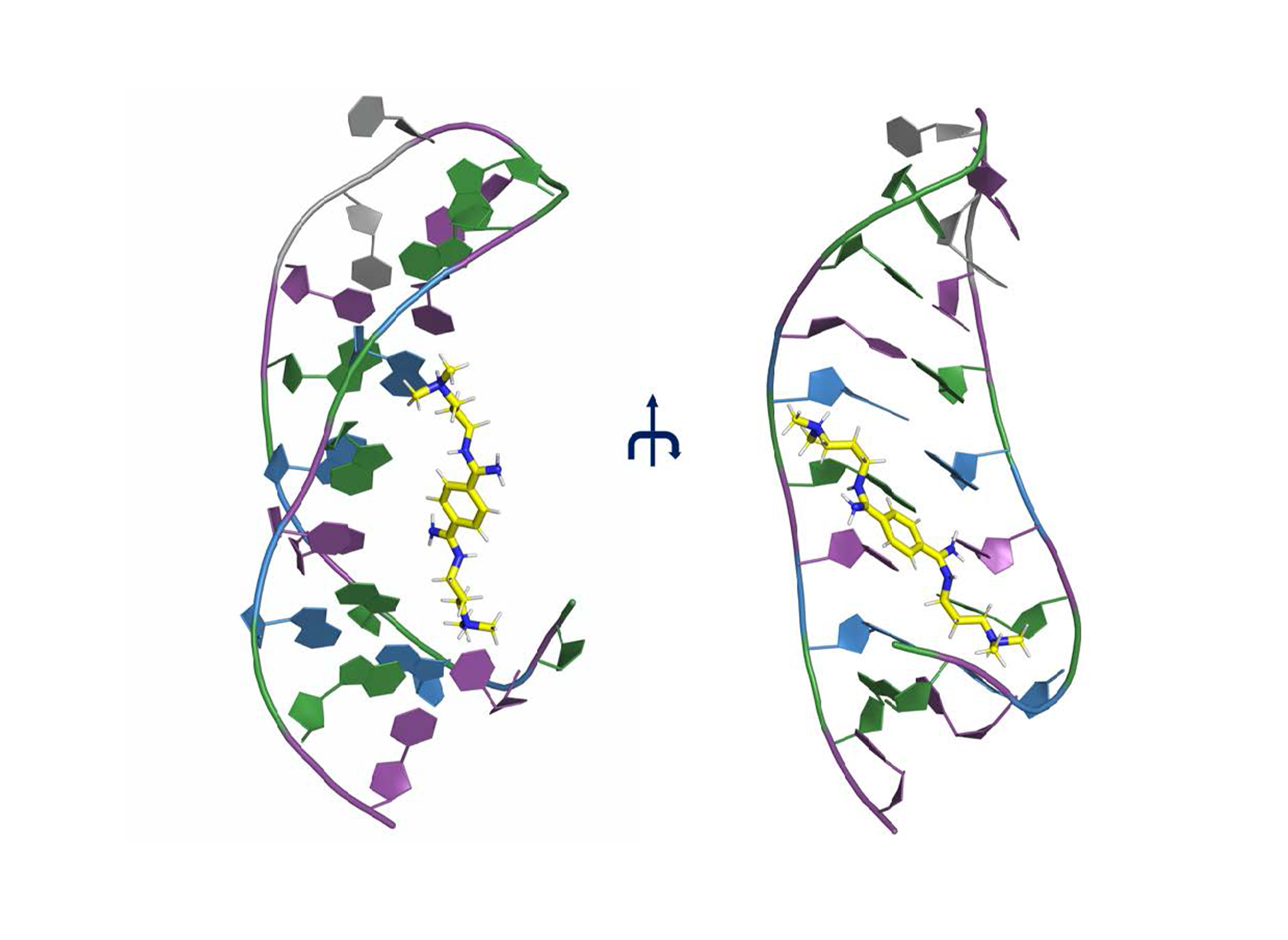 Figure 1. CAG hairpin complex with the ligand DB213 [18]. The ligand is represented in yellow stick, while the CAG RNA is represented in cartoon (C: Violet, A: Blue, G: Green, U: Gray). The structure forms a hairpin.
Figure 1. CAG hairpin complex with the ligand DB213 [18]. The ligand is represented in yellow stick, while the CAG RNA is represented in cartoon (C: Violet, A: Blue, G: Green, U: Gray). The structure forms a hairpin. 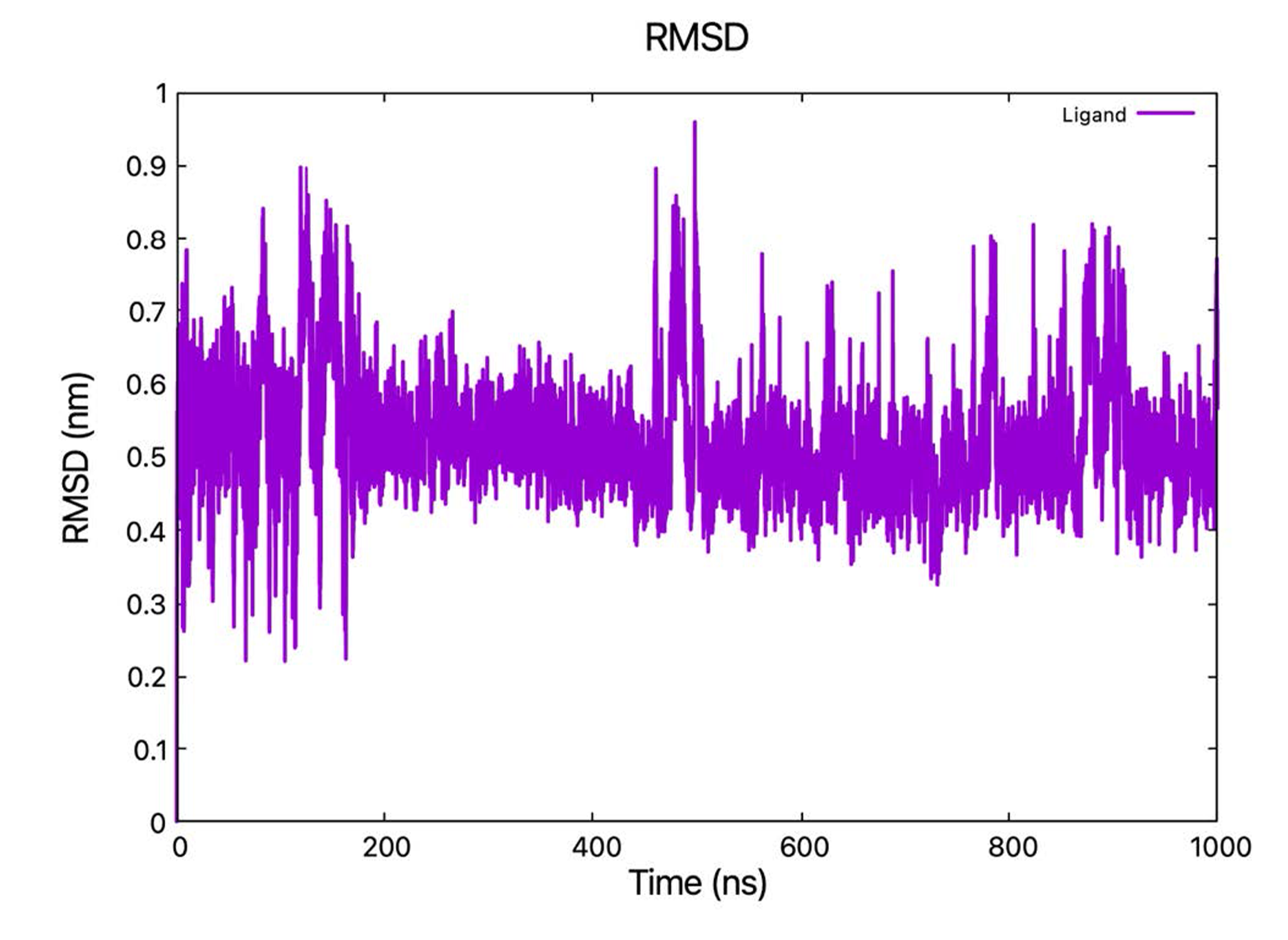 Figure 2. RMSD of the DB213 ligand relative to the starting structure as a function of simulated time during the classical MD (fitting the RNA backbone to the structure after equilibration phase every time step).
Figure 2. RMSD of the DB213 ligand relative to the starting structure as a function of simulated time during the classical MD (fitting the RNA backbone to the structure after equilibration phase every time step). 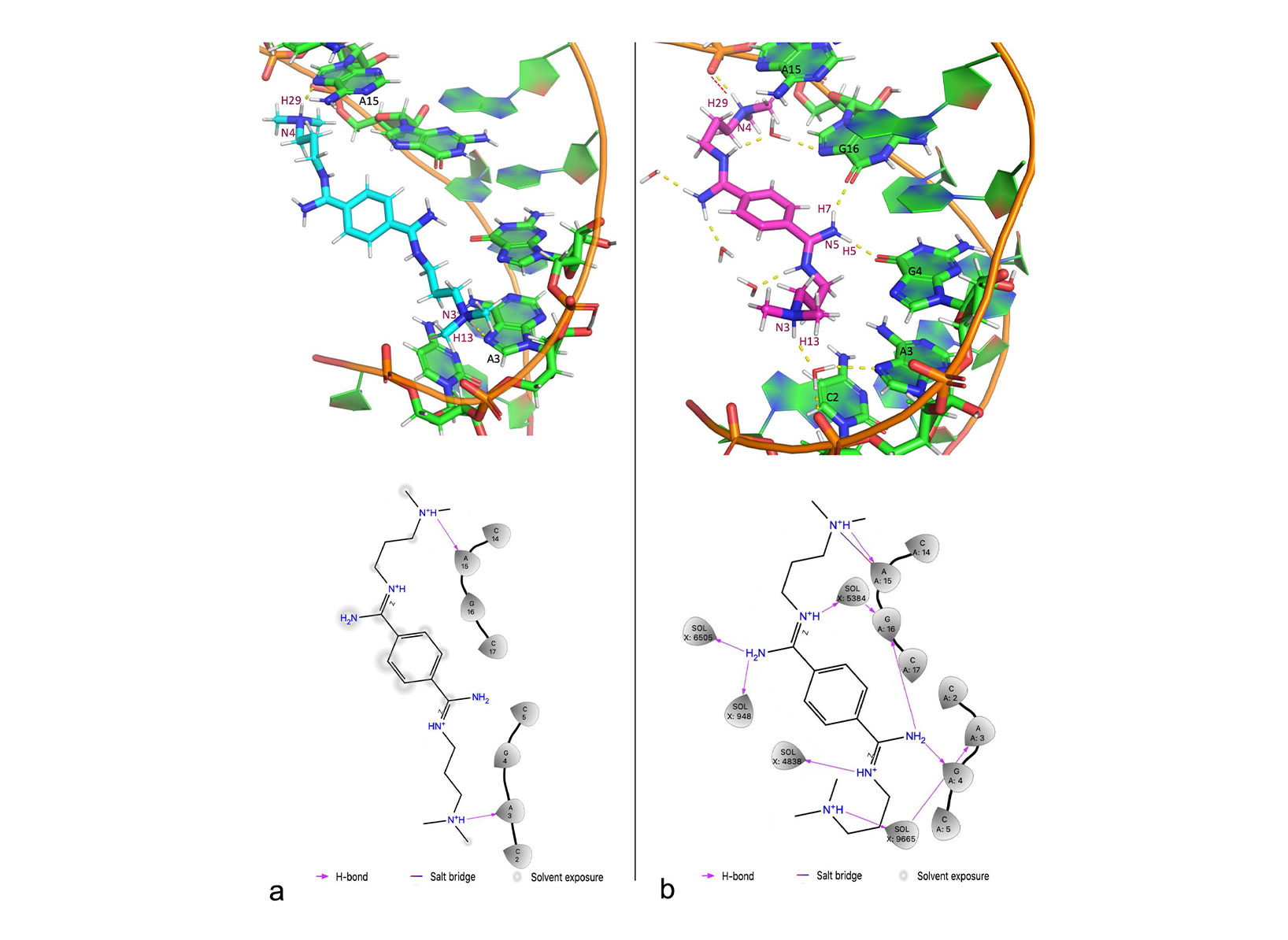 Figure 3. (a) Intermolecular interactions between CAG RNA and DB213 ligand in NMR1 structure. Upper: the 3D structure, in which H-bonds are drawn as yellow dashed lines. Lower: DB213/ CAG RNA interaction diagram. (b) Intermolecular interactions between CAG RNA and DB213 ligand in QM/MM MD. Upper: the 3D structure, in which H-bonds are drawn as yellow dashed lines and salt bridges are drawn as red dashed lines. Lower: DB213/ CAG RNA interaction diagram.
Figure 3. (a) Intermolecular interactions between CAG RNA and DB213 ligand in NMR1 structure. Upper: the 3D structure, in which H-bonds are drawn as yellow dashed lines. Lower: DB213/ CAG RNA interaction diagram. (b) Intermolecular interactions between CAG RNA and DB213 ligand in QM/MM MD. Upper: the 3D structure, in which H-bonds are drawn as yellow dashed lines and salt bridges are drawn as red dashed lines. Lower: DB213/ CAG RNA interaction diagram. 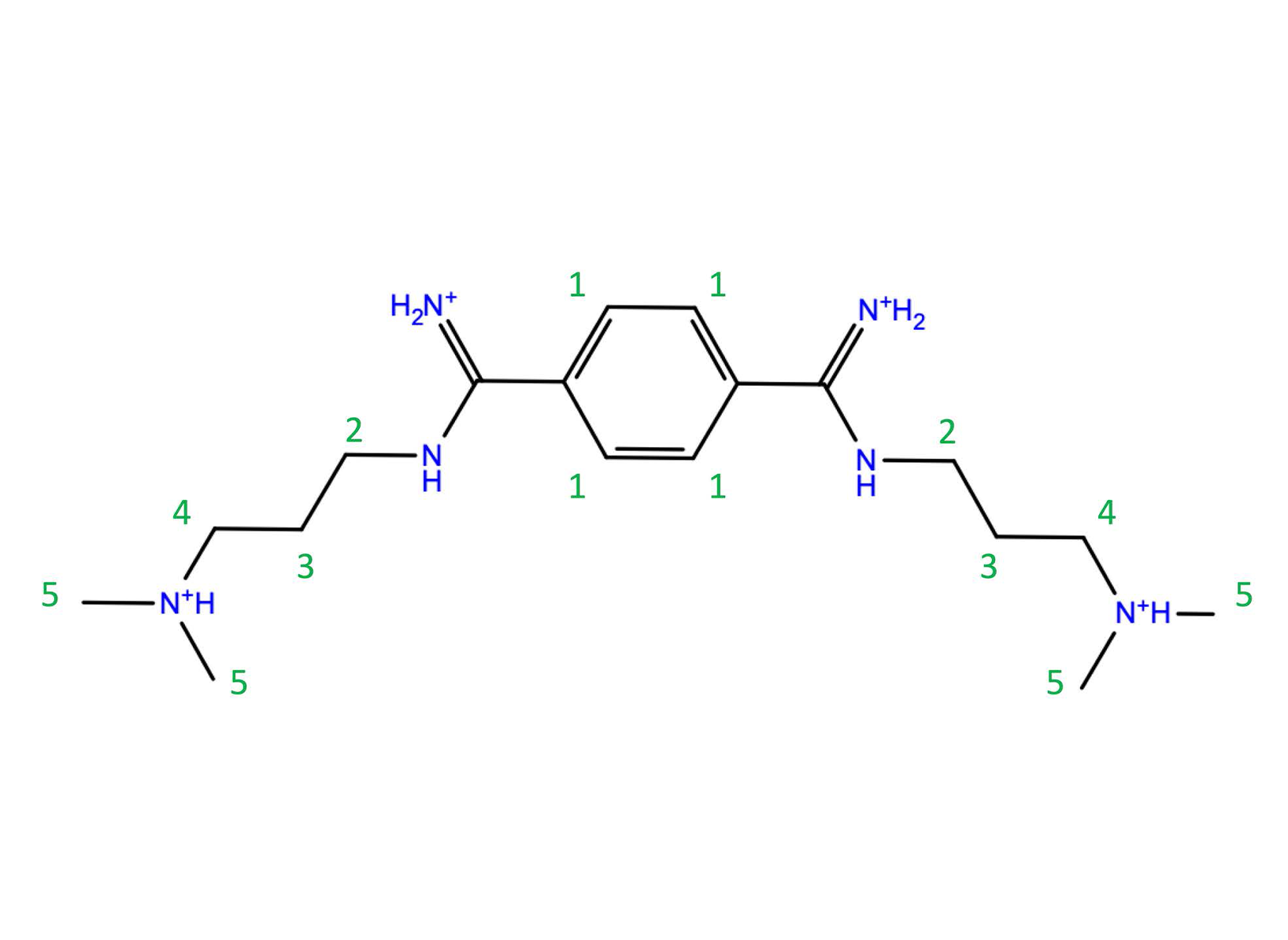 Chart 1. The structure of DB213 ligand. The numbers in green are labels for NMR chemical shifts experiment (Table 1).
Chart 1. The structure of DB213 ligand. The numbers in green are labels for NMR chemical shifts experiment (Table 1). 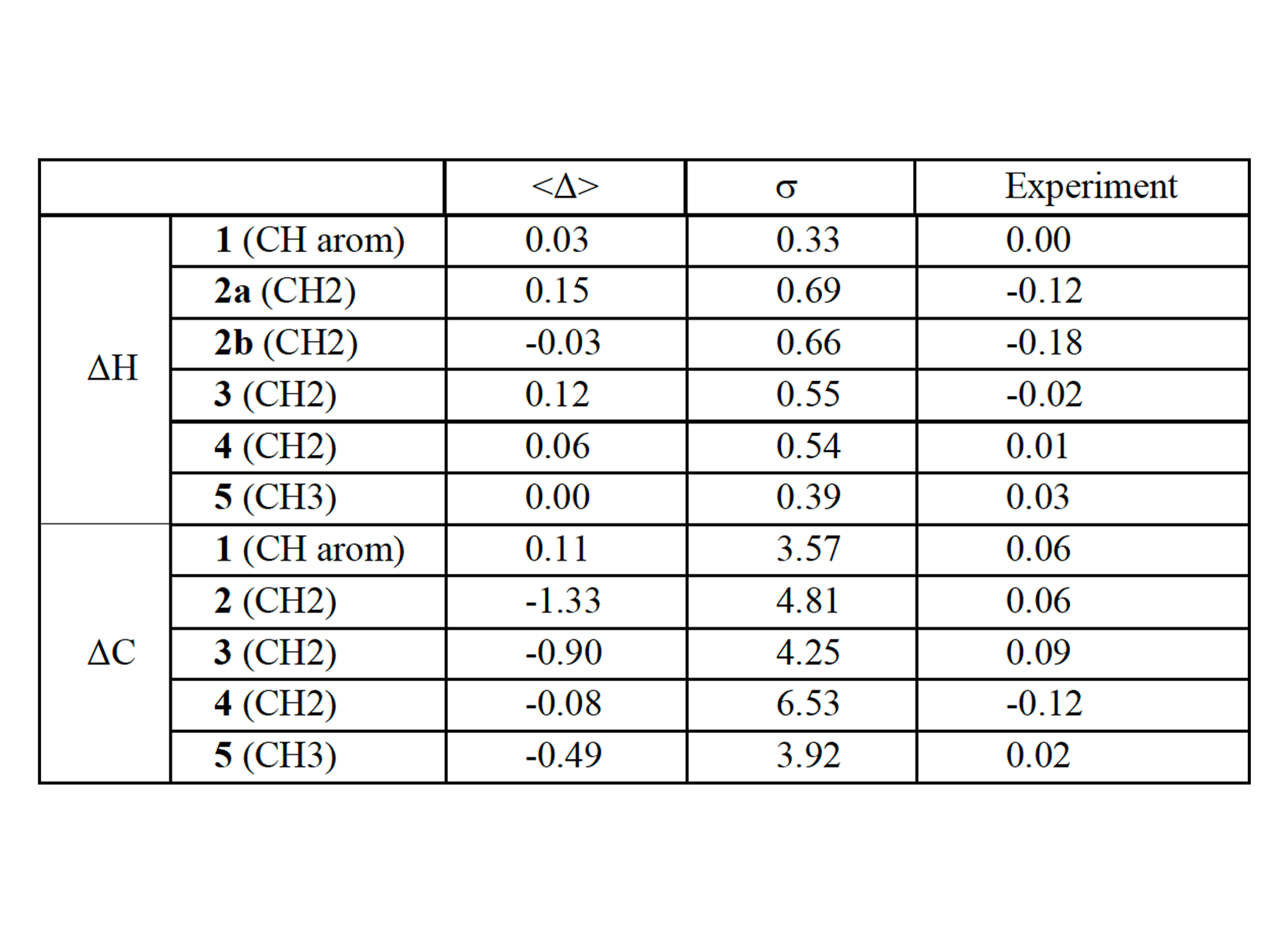 Table 1. Changes in 1H (ΔH) and 13C (ΔC) chemical shifts of the DB213 ligand on passing from water to RNA-bound state (ppm) in comparison with NMR chemical shifts experiment. The atoms’ labels are reported in chart 1. 2a, 2b refer to the two diastereotopic protons of this CH2 group. The averaged values (<Δ>) over 250 snapshots (last 60 ps) during QM/MM
MD and the corresponding standard deviations (s) are also reported.
Table 1. Changes in 1H (ΔH) and 13C (ΔC) chemical shifts of the DB213 ligand on passing from water to RNA-bound state (ppm) in comparison with NMR chemical shifts experiment. The atoms’ labels are reported in chart 1. 2a, 2b refer to the two diastereotopic protons of this CH2 group. The averaged values (<Δ>) over 250 snapshots (last 60 ps) during QM/MM
MD and the corresponding standard deviations (s) are also reported. 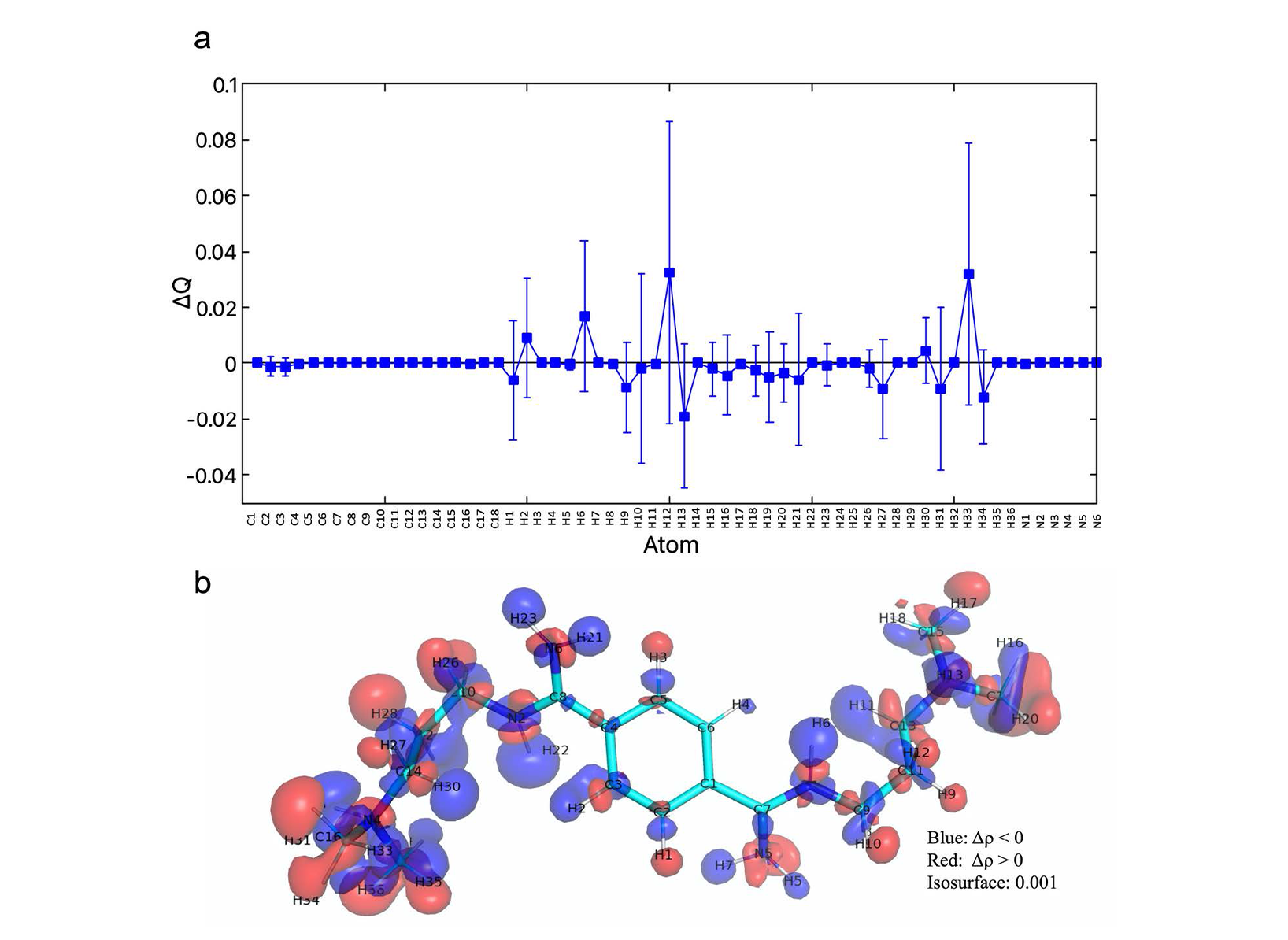 Figure 4. (a) Changes in atomic charge calculated for each atom of the ligand (including average value and deviation) during the last 60 ps of the QM/MM simulation RNA/ligand complex. (b) Changes in electronic density Δr (RNA – vacuum) of the ligand on passing from in vacuum to in RNA-bound state. The structure is taken from a QM/MM simulation snapshot.
Figure 4. (a) Changes in atomic charge calculated for each atom of the ligand (including average value and deviation) during the last 60 ps of the QM/MM simulation RNA/ligand complex. (b) Changes in electronic density Δr (RNA – vacuum) of the ligand on passing from in vacuum to in RNA-bound state. The structure is taken from a QM/MM simulation snapshot.